Clustering behavior summary of dynamic metric data via Persistent Homology
When studying flocking/swarming behaviors in animals one is interested in quantifying and comparing the dynamics of the clustering induced by the coalescence and disbanding of animals in different groups.
Motivated by this, we study the problem of obtaining persistent homology based summaries of time-dependent metric data.
Given a finite dynamic metric space (DMS), we construct the zigzag simplicial filtration arising from applying the Rips simplicial complex construction (with a fixed scale parameter) to this finite DMS. Upon passing to 0-th homology with field coefficients, we obtain a zigzag persistence module and, based on standard results, we in turn obtain a persistence diagram or barcode from this zigzag persistence module.
We prove that these barcodes are stable to perturbations in the DMSs space under a certain varaint of the Gromov-Hausdorff distance we construct [1] by exploiting the algebraic stability of zigzag persistence by M. Botnan and M. Lesnick [2] and improvement by H.B. Bjerkevik [3] .
Along the way, we propose a summarization of dynamic metric spaces that captures their time-dependent clustering features which we call formigrams (zigzag-generalization of dendrograms).
This work was partially supported by NSF grants IIS-1422400 and CCF-1526513.
Example: Formigram generated by trajectories on the real line
The figure below consists of three diagrams exemplify a formation of formigram. All the x-axes are time.
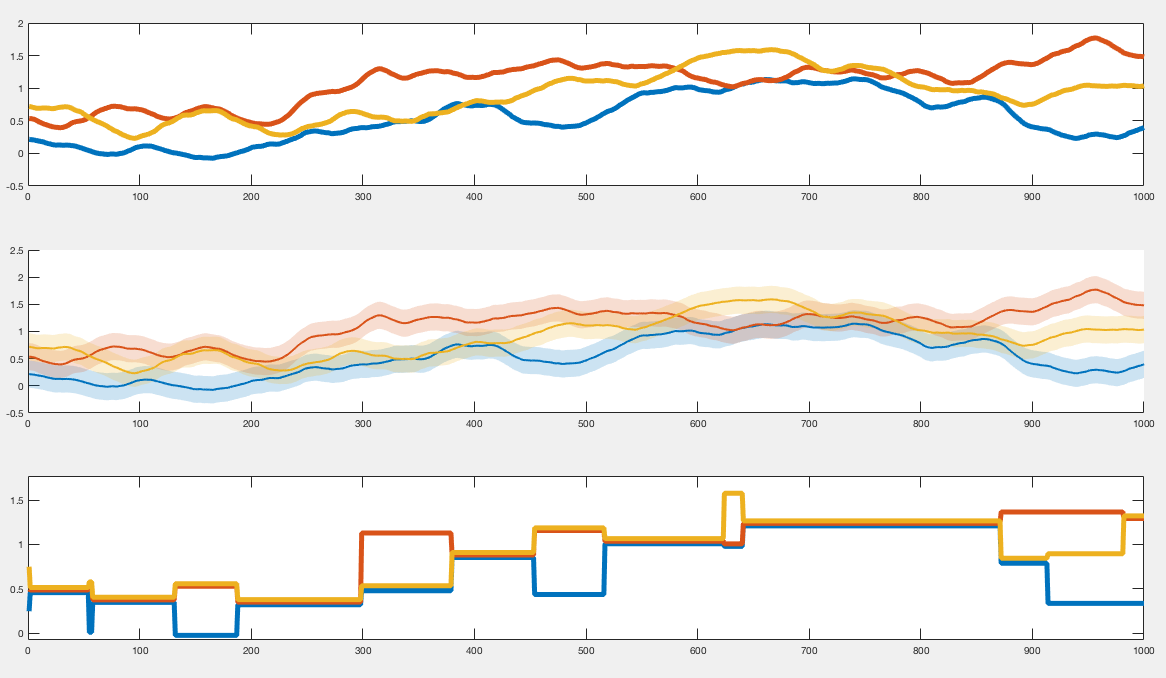
The 1st row: The y-axis is the real line as a metric space. This diagram illustrates the trjactories of 3 moving points (blue, red, yellow) over time.
The 2nd row: For a fixed δ >0, this diagram represents δ-thickened trajectories of the first diagram.
The 3rd row: At each time, a partition on the set { blue, red, yellow } of points is formed according to the following rule: Two points are contained in the same block if their δ-thickend trajectories intersect. In this third diagram, y-axis does not have any meaning.
The movie below shows both the dynamic graph overlaid on the dynamic point cloud (on the left) and the resulting formigram (on the right).
Examples: 4 different behaviors in flocking model
The following videos show some examples of 4 different flocking behaviors on a flat torus caused by different parameter settings. (We computed these by modifying the code of Boids) In this flocking model, the behaviors of individual entities are governed by tuning the following parameters: separation (tendency not to be close to each other) , alignment (tendency to synchronize their velocity with their neighbors), and cohesion (tendency to move toward the average position of local flockmates).
Behavior 1
Behavior 2
Behavior 3
Behavior 4
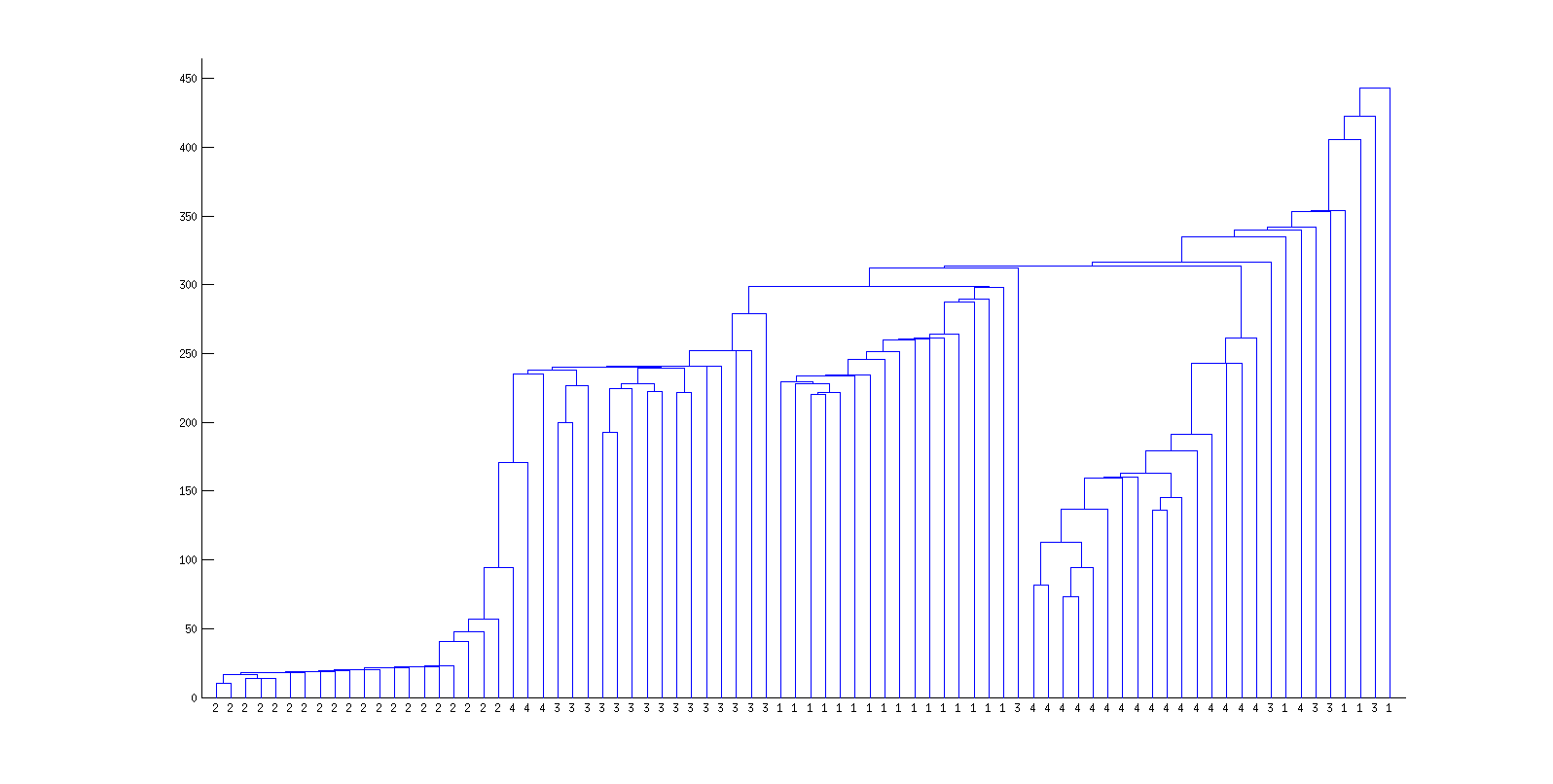
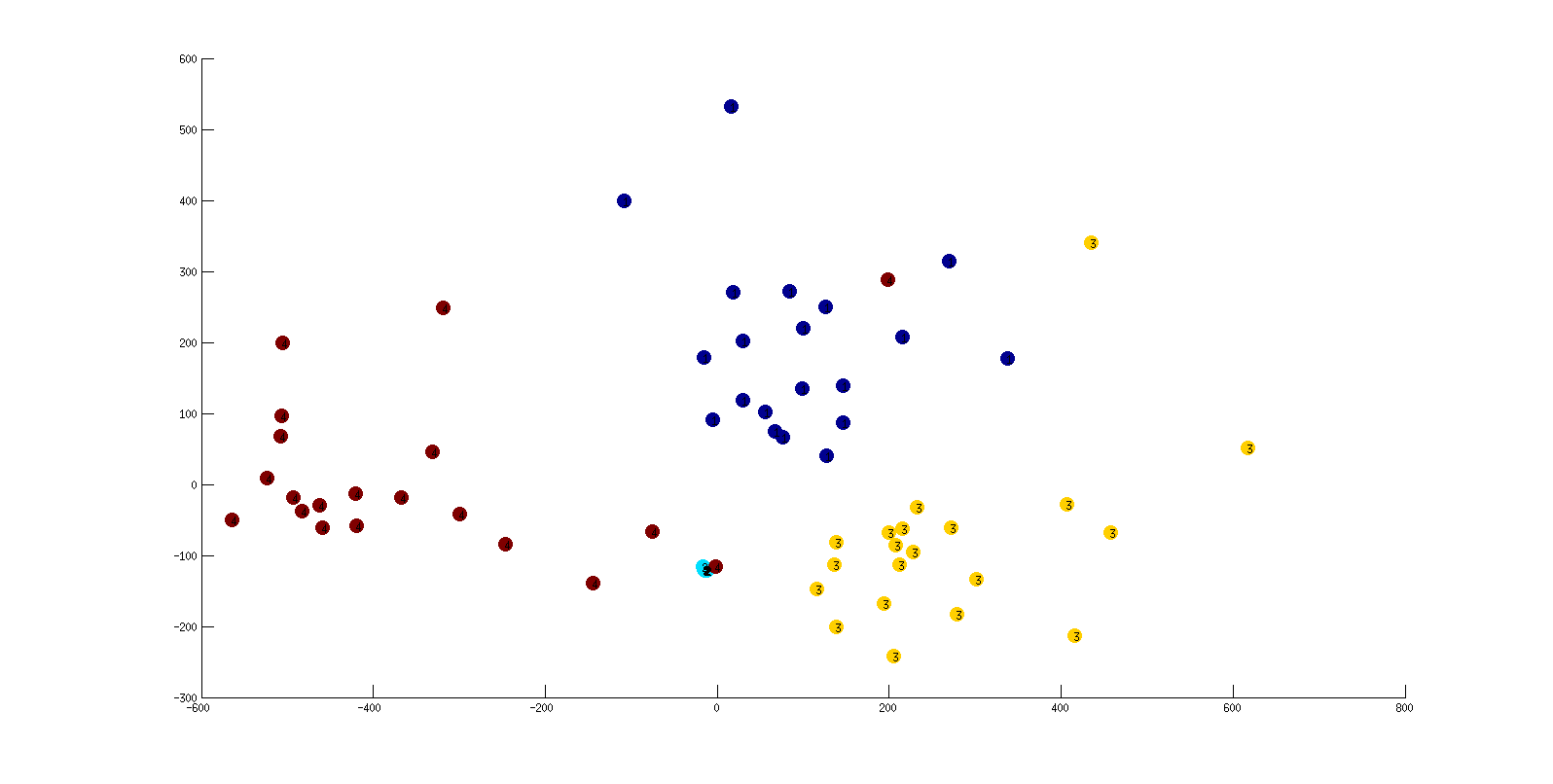
With specific choices of these parameters, we run simulation 20 times (with random initial configuration) and generated their clustering barcodes. After that, via the Single Linkage Hierarchical Clustering and MDS, using the bottleneck distance, 4 behaviors were quite well distinguished (see the dendrogram and the MDS plot below).
These compuational results were produced by Zane Smith, a graduate student in Computer Science and Engineering at University of Minnesota.
Results
In the following dendrogram and MDS plot, each index of 1,2,3 or 4 stands for an instance of Behaviors 1,2,3 or 4, respectively. Note especially that barcodes from instances of Behavior 4 are very tightly clustered in both the dendrogram and MDS plot. (For the case you cannot see clearly the indices in the MDS plot below are navy=1, light blue=2, yellow= 3, red=4).
Dendrogram
MDS plot
Noah Veltman's Flocking Boids
Relevant Links
- W. Kim, F. Memoli (2017), Stable Signatures for Dynamic Graphs and Dynamic Metric Spaces via Zigzag Persistence, arXiv:1712.04064
- W. Kim, F. Memoli (2018), Formigrams: Clustering Summaries of Dynamic Data, Proceedings of Canadian Conference on Computational Geometry 2018
- W. Kim, F. Memoli (2018), Spatio-temporal persistent homology for dynamic metric spaces, arXiv:1812.00949
- W. Kim, F. Memoli, A. Stefanou (2019) The metric structure of the formigram interleaving distance, arXiv:1912.04366
- M. Botnan, M. Lesnick (2017), Algebraic Stability of Zigzag Persistence Modules, arxiv:1604.00655
- H.B. Bjerkevik (2016), Stability of higher-dimensional interval decomposable persistence modules, arxiv:1609.02086
- Buchin et al (2014), Trajectory Grouping Structure
- Flocking of birds video, https://vimeo.com/ondemand/130410
- Swarming/Flocking pictures, http://www.xavibou.com/index.php/project/ornitographies/
- Topaz et al (2015), Topological Data Analysis of Biological Aggregation Models
- Elizabeth Munch Ph.D. thesis (2013), Applications of Persistent Homology to Time Varying Systems
- David J.T. Sumpter, Collective Animal Behavior